排序算法整理

发表于 | 分类于

前言

　　排序一直是算法中的经典和入门，也是一个合格的程序员应该随手都能够回答的问题。但是现实是，不经常写，不经常用的话，要是一下子让写或者让讲，估计有一半的人会呛住。

　　在前年求职之前，系统的复习过所有经典的排序算法，也可以做到随手写出来的地步，但是前几天接触，突然发现自己都忘的差不多了，可能随手可以写个，选择，冒泡，插入排序，但是堆排（只知道最大堆的特性，基本忘记），快排和归并（只知道思路），所以写这篇文章的目的就是再重新花几天时间系统的再整理一下，复习一下，也以便于后续的温习。

概况

　　排序顾名思义就是将一堆杂乱无章的数字，按照一定的规则（最大或者最小）进行排列的过程。

排序的分类

  • 按照是否将所有的记录全部加载到内存中进行排序分为：内部排序和外部排序

    img

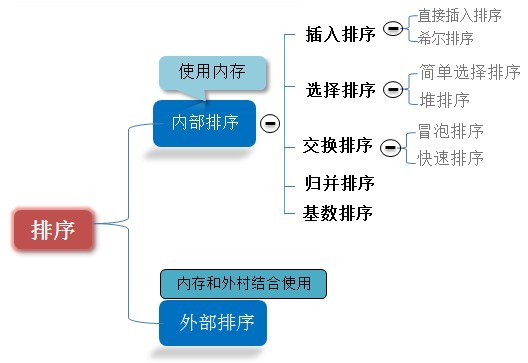
  • 按照排序是否稳定分为：稳定排序和不稳定排序

    何谓稳定性？

    假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

  • 按照原理可以分为：插入排序，选择排序，交换排序，归并排序和基数排序

排序的方式

　　经典的排序算法大致有以下10种

排序方法 时间复杂度（平均） 时间复杂度（最坏) 时间复杂度（最好) 空间复杂度 稳定性 复杂性
直接插入排序 O(n2) O(n2) O(n) O(1) 稳定 简单
希尔排序 O(nlog2n) O(n2) O(n) O(1) 不稳定 较复杂
直接选择排序 O(n2) O(n2) O(n2) O(1) 不稳定 简单
堆排序 O(nlog2n) O(nlog2n) O(nlog2n) O(1) 不稳定 较复杂
冒泡排序 O(n2) O(n2) O(n) O(1) 稳定 简单
快速排序 O(nlog2n) O(n2) O(nlog2n) O(nlog2n) 不稳定 较复杂
归并排序 O(nlog2n) O(nlog2n) O(nlog2n) O(n) 稳定 较复杂
基数排序 O(d(n+r)) O(d(n+r))) O(d(n+r)) O(n+r) 稳定 较复杂

详情

插入排序

概念和原理

插入排序简单的讲就是从一堆无序的数据集中取出一个数，加入到有序的数据集中，直到所有的无序数据集都取完，那么有序的数据集就是排序后的数。

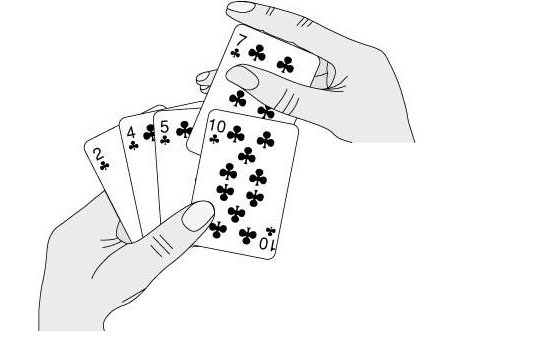
1527263835518

如上图所示，形象的解释了插入排序的原理。开始时，我们的左手为空并且桌子上的牌面向下，然后我们每次从桌子上拿走一张牌并将他们插入到左手中正确的位置，插入排序的原理由此而得。

思想

输入： 数组 A[1….n]

步骤：

​ 使用j作为标志位，j的左边为有序的数字，后边为无序的数字，那么初始j=2，最后n结束;

​ key=A[j]作为待插入的值，假设待加入的值是有序数组中的最大值，那么他的位置应该不变，那么如果不是呢？那么应该从有序数组的最后一个数A[i=j-1]（有序数组中的最大值）进行比较，如果小，那么把这个大的数插入到j处，依次直到i>0&key>A[i]，继续下一轮。

一句话概括：插入排序就是增熵减熵的过程

伪码
1
2
3
4
5
6
7
8
9
10
INSERTION-SORT(A)
// INSERTION-SORT
 for j=2 to A.length
     key = A[j]
     //insert A[j] into the sorted sequence A[1...j-1]
     i = j-1;
     while i>0 and A[i]>A[j]
        A[i+1] = A[i]
        i = i-1
     A[i+1] = key
实现

JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int[] insert_sort(int []arrs){
      for(int j=1;j<arrs.length;j++){
          int key = arrs[j];
          int i = j-1;
          while(i>=0&&arrs[i]>key){
              arrs[i+1] = arrs[i];
              i--;
          }
          arrs[i+1] = key;
      }
      return arrs;
  }

  public static void main(String[] args) {
      int res[] = new Sort().insert_sort(new int[]{199,1,2,8,3});
      for (int e : res) {
          System.out.println(e);
      }
  }

1527412551814

JAVASCRIPT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var insert_sort = function (arrs){
	for(var j=1;j<arrs.length;j++){
		var key = arrs[j];
		var i = j-1;
		while(i>=0&&arrs[i]>key){
			arrs[i+1] = arrs[i];
			i--;
		}
		arrs[i+1] = key;
	}
}
var a = [199,1,2,8,3];
insert_sort(a)
console.log(a)  //1,2,3,8,199

时间复杂度

//todo

空间复杂度

//todo

稳定性

//todo

希尔排序

选择排序

概念和原理

选择排序就是就是从一堆数字中取出一个最小的放在一边，然后再去取一个最小的数，跟刚刚取出来的数字放一起，这样直到这堆数字被取完位置。

形象一点比如皇帝翻牌:heart_eyes_cat:，皇帝一天公务繁忙，晚上到了，这个时候太监就会走过来拿着下面的牌子让他选，这个是否皇帝会看一下都有哪些牌子，然后选择他最喜欢的一个妃子；如果皇帝觉得今天一个不够，还需要一个那么皇帝会在剩下的当中选择在他心中地位其次的妃子。

这个时候老佛爷说，皇帝你再选一个，这个时候皇帝又会在剩下的当中选择一个最好的。

1527414146675

皇帝选秀就是一个典型的选择排序问题

　　现实生活中选择排序的思想运用的很多：挑衣服，挑零食等等，感觉选择排序的思想有点像贪心算法。

思路

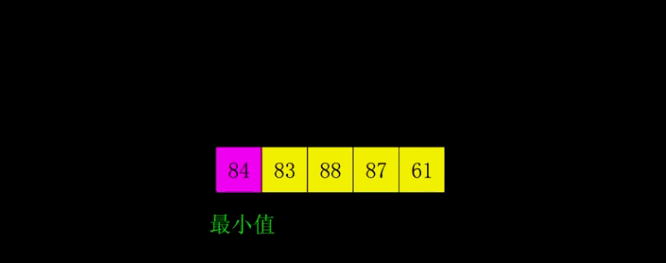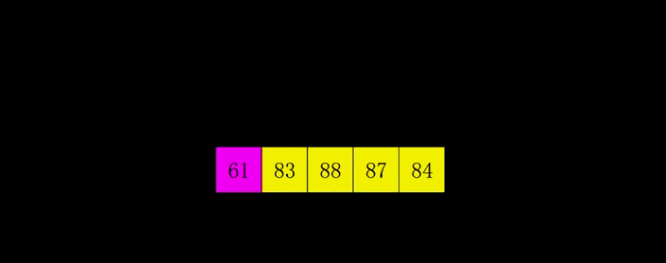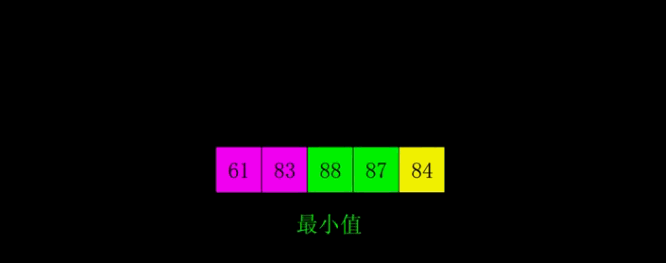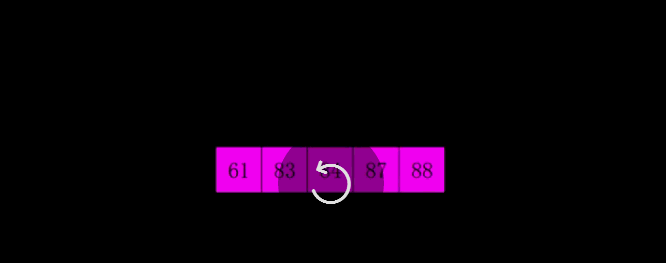
1527413889306

该图阐述了选择排序的思想，从数组中遍历求出最小值，然后与连续的数组开头的组相互调换，直到所有的数都有序，排序结束

伪码
1
2
3
4
5
6
7
8
9
10
SELECTION-SORT(A)                        
   for j = 1 to Length(A)                            
       i = j                                                         
       key = A(i)                                              
       for i to Lenth(A)                                   
          if key>A(i)                                         
                key = A(i)   //当前最小值                                
                k = i        // 当前最小值的坐标                                  
       A(k) = A(j)     //把游标位置的数放到最小值的位置中区                                        
       A(j)  = key     //把最小值放入指定的游标位置
实现

JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public void select_sort(int[] a) {
       if (a == null || a.length <= 0) {
           return;
       }
       for (int i = 0; i < a.length; i++) {
           int temp = a[i];
           int flag = i; // 将当前下标定义为最小值下标
           for (int j = i + 1; j < a.length; j++) {
               if (a[j] < temp) {// a[j] < temp 从小到大排序；a[j] > temp 从大到小排序
                   temp = a[j];
                   flag = j; // 如果有小于当前最小值的关键字将此关键字的下标赋值给flag
               }
           }
           if (flag != i) {
               a[flag] = a[i];
               a[i] = temp;
           }
       }
   }

   public static void main(String[] args) {
       int res[] = new int[] { 199, 1, 2, 8, 3 }; // 1,2,3,8,199
       new Sort().select_sort(res);
       for (int e : res) {
           System.out.println(e);
       }
   }

JAVASCRIPT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
var select_sort = function(arrs) {
        if (arrs == null || arrs.length <= 0) {
            return;
        }
        for (var i = 0; i < arrs.length; i++) {
            var temp = arrs[i];
            var flag = i; // 将当前下标定义为最小值下标
            for (var j = i + 1; j < arrs.length; j++) {
                if (a[j] < temp) {// a[j] < temp 从小到大排序；a[j] > temp 从大到小排序
                    temp = a[j];
                    flag = j; // 如果有小于当前最小值的关键字将此关键字的下标赋值给flag
                }
            }
            if (flag != i) {
                a[flag] = a[i];
                a[i] = temp;
            }
        }
    }
var a = [199,1,2,8,3]; // 1,2,3,8,199
select_sort(a)
console.log(a)
时间复杂度

选择排序交换此处是处于0-（n-1）次之间，需要比较n(n-1) / 2次，赋值操作次数在0-3(n-1)次之间，因此平均时间复杂度为O(n2)

空间复杂度

O(1)

稳定性

序列{5 8 5 2 9}， 我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法

注：一般认为选择排序是不稳定排序，但是如果开辟一个新数组的话可以保证稳定性

冒泡排序

概念与原理

​ 冒泡的核心是一次bubble的过程，如下图所示，数组A[1…n]进过n-1次bubble过程就可以完成排序。

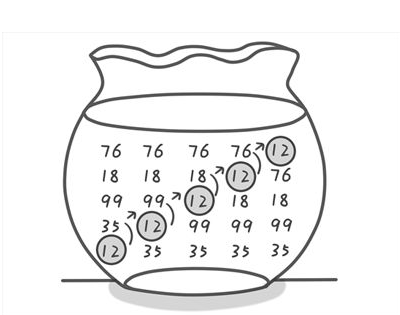
1527419114353

图中描述的是一次气泡（bubble）过程，小气泡12与相邻的对比，如果自己小，那么向上冒泡，一次冒泡过程就可以把最小的数冒泡到最上层。其余的无序数组也是利用类似的思想进行排序

伪码
1
2
3
4
5
BUBBLESORT(A)  
    for i = 1 to A.length-1   //总共bubble n-1次
        for j = A.length downto i + 1  //bubble的范围
            if A[j] < A[j - 1]  
                exchange A[j] with A[j - 1]  //bubble的过程
实现

JAVA

1
2
3
4
5
6
7
8
9
10
11
public void bubble_sort(int []a){
       for(int i=0;i<a.length-1;i++){
           for(int j=0;j<a.length-1-i;j++){
               if(a[j+1]<a[j]){
                   int temp = a[j+1];
                   a[j+1] = a[j];
                   a[j] = temp;
               }
           }
       }
   }

JAVASCRIPT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var bubble_sort = function(a){
        for(var i=0;i<a.length-1;i++){
            for(var j=0;j<a.length-1-i;j++){
                if(a[j+1]<a[j]){
                    var temp = a[j+1];
                    a[j+1] = a[j];
                    a[j] = temp;
                }
            }
        }
}
var arrs = [76,18,99,35,12];
bubble_sort(arrs);
console.log(arrs);//12,18,35,76,99
时间复杂度

1527425711208

摘自百度百科

空间复杂度

O(1)

稳定性

冒泡排序比较是相邻的两个元素，交换也发生在这两个元素中。如果两个元素相等，不交换；如果两个相等元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。